Notice
Recent Posts
문제 풀이 및 개발 공간
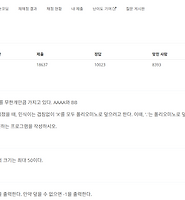
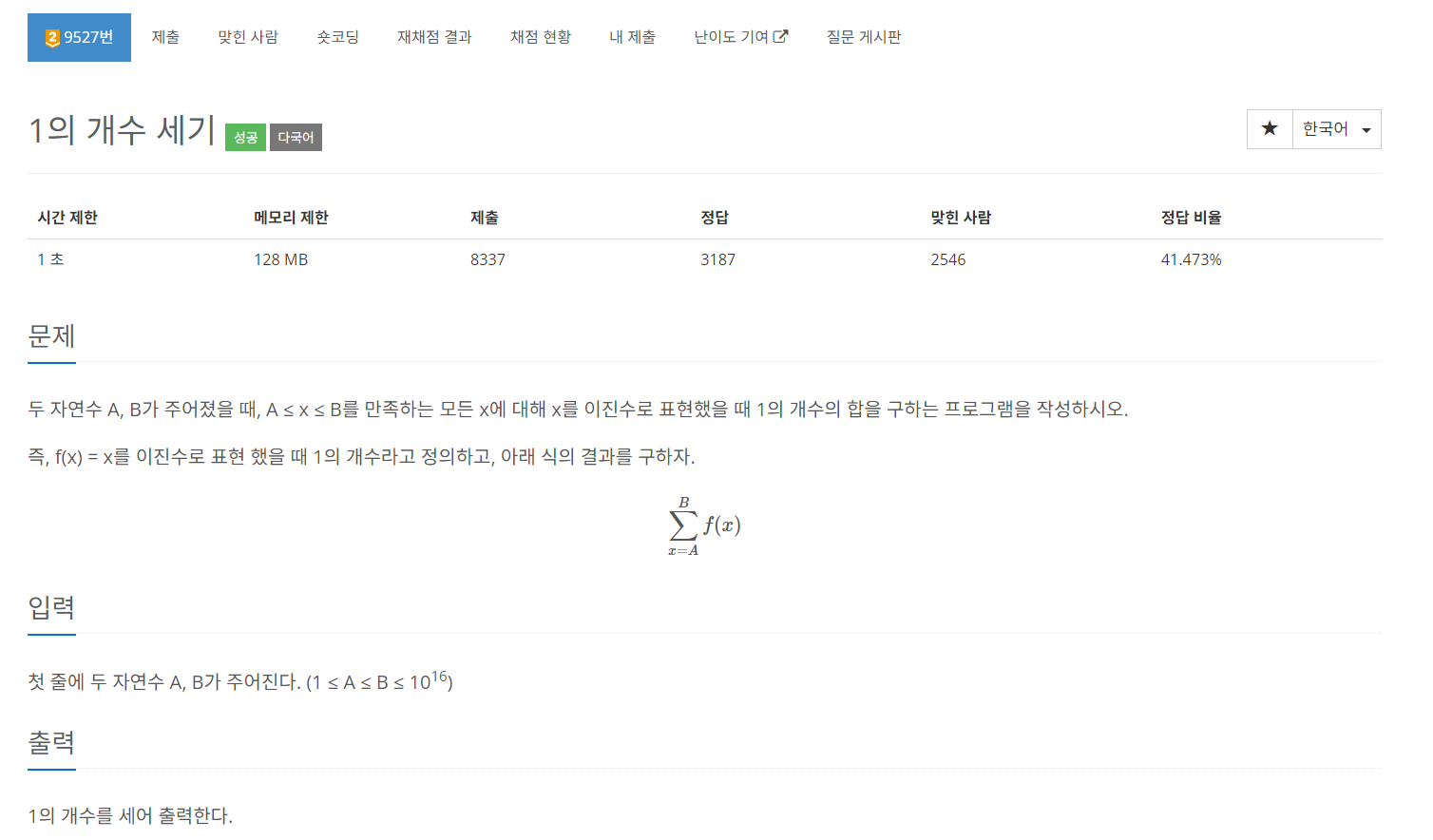
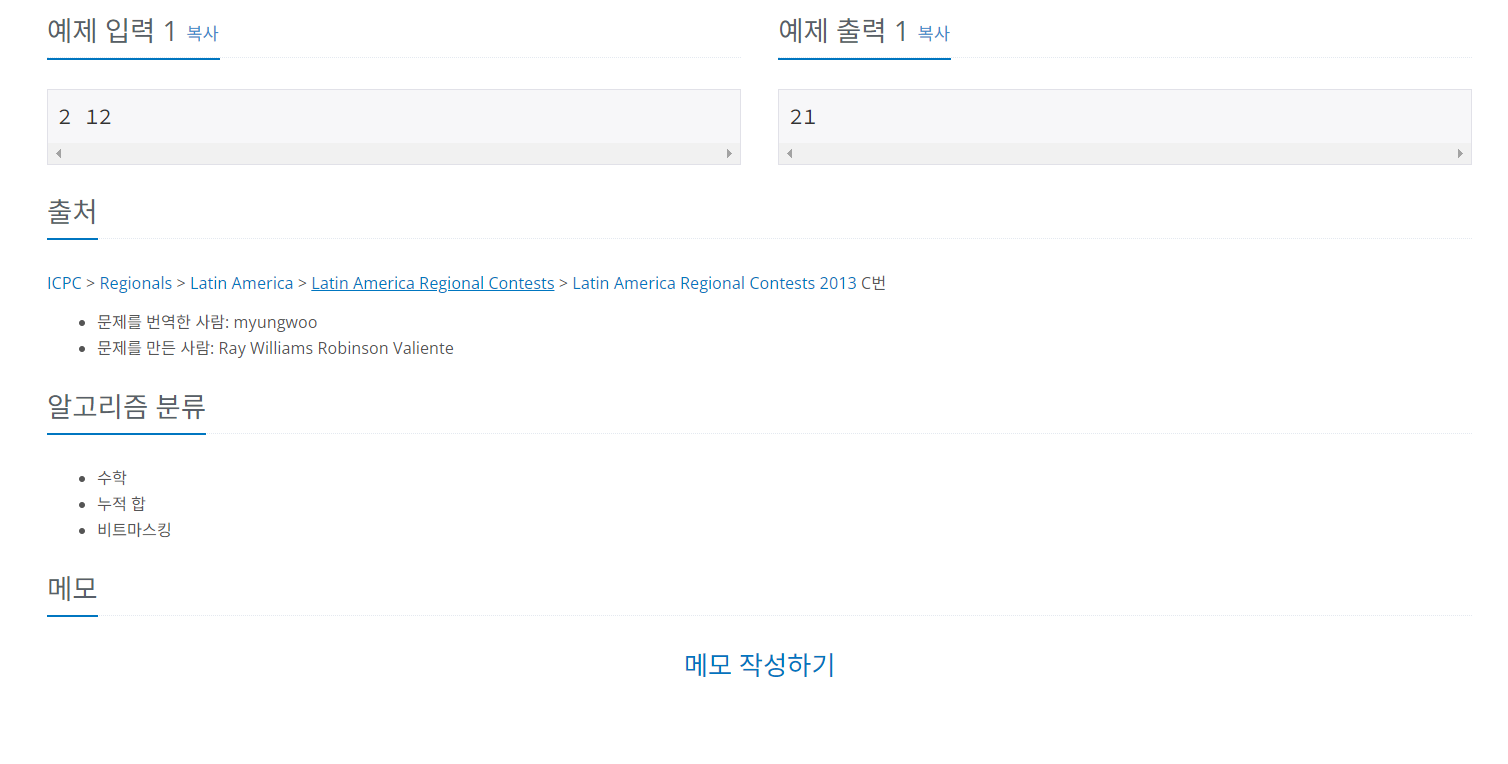
[백준] 9527번 1의 개수 세기 (gold 2 본문
import java.io.*;
import java.util.*;
public class Main{
static HashMap<Long,Long> dict=new HashMap<>();
static ArrayList<Long> arr;
public static void main(String[] args) throws IOException{
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
long s=Long.valueOf(st.nextToken());
long e=Long.valueOf(st.nextToken());
init(e);
arr=new ArrayList<>(dict.keySet());
Collections.sort(arr);
//1에서 끝점. s에서 시작하므로 s는 포함이므로,
//1에서 s-1까지의 범위를 빼면 된다.
long answer=solve(1,e)-solve(1,s-1);
System.out.println(answer);
}
//규칙이 존재한다. 1은 이진수로 1, 2는 10 3은 11,
//4는 100, 5는 101, 6은 110, 7은 111.
//잘보면 4,5,6,7은 4의 100에 1,2,3 이진수를 합친 것과 같다.
//다음의 범위 8-15는 10000뒤에, 1-7까지를 더한 것과 같은 것이다.
//이러한 규칙을 적용하여, end까지의 규칙에 맞게 해당 수들을 구한다.
//이러한 과정을 진행하면, 2,4,6,8은 이진수 자리수가 늘어나게 되면서.
//약간의 규칙이 깨지므로, 2,4,6,8전의 1,3,5,7로 규칙을 적용하여 계산해 나가고,
//이 수에 +1을 한 값 즉, 2,4,6,8경계까지의 값도 추가해준다.
public static void init(Long e){
dict.put(0L,0L);
dict.put(1L,1L);
dict.put(2L,2L);
long n=2;
while(n<=e){
long temp=n*2;
dict.put(temp-1, dict.get(n-1)*2+n);
dict.put(temp, dict.get(temp-1)+1);
n=temp;
}
}
public static long solve(long start, long end){
if(end==0){
return 0;
}
else if(end==1){
return 1;
}
//end를 넘지않는 2의 배수중 가장 큰 수
//수가 홀 짝 순으로 되어있다보니, 그 전 2의 배수를 찾으려면 i-2
long find=0L;
for(int i=0; i<arr.size(); i++){
long temp=arr.get(i);
if(temp%2==0 && temp>end){
find=arr.get(i-2);
break;
}
}
//로직은 다음과 같다. end가 있으면, end 보다 작으면서 가장 가까운 2의 배수까지의
//합을 더하고, 그 뒤부터 end까지의 범위를 구한다. 이때,
//나머지 범위들은 이 전보다 이진수 1이 하나 추가되므로, 갯수(end-find만큼
//추가된 1을 더해주고, 나머지를 solve로 보내서 구한다.
//1-12까지 더한다고 가정한다면.
//1-8은 위에서 구한 1-8까지의 합이다.
//9-12를 구해야 하는데, 9는 1001, 10은 1010, 11은 1011, 12는 1100이다.
//이는 바꾸면 8(1000)+1(1), 8(1000)+2(10), 8(1000)+3(011), 8(1000)+4(100)
//인 것이다. 바꾸어 말하면, 최대 2의 배수 범위까지 구하면, 뒤의 범위는,
//12-8=4, 1-4구간과 동일한 것이다. 단지, 1-4구간에 맨 앞에 1이진수 (8)의 값이 추가된 것만 차이이다.
return dict.get(find)+(end-find)+solve(1, end-find);
}
}'백준공부 > java' 카테고리의 다른 글
| [백준] 1343번 폴리오미노 (silver 5 (0) | 2024.09.03 |
|---|---|
| [백준] 4179번 불! (gold 3 (0) | 2024.06.27 |
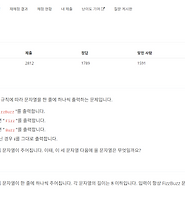
| [백준] 28702번 FizzBuzz (bronze 1 (0) | 2024.06.27 |
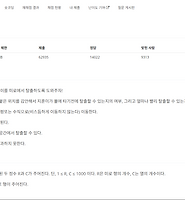
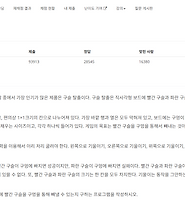
| [백준] 13460번 구슬 탈출 2 (gold 1 (0) | 2024.06.26 |
| [백준] 15683번 감시 (gold 3 (0) | 2024.06.25 |